- 注意坐标系旋转不同于坐标点旋转
- 坐标系旋转角度θ则等同于将目标点围绕坐标原点反方向旋转同样的角度θ
1.三维坐标系推导过程
假设三维坐标系是一个右手坐标系。如下图
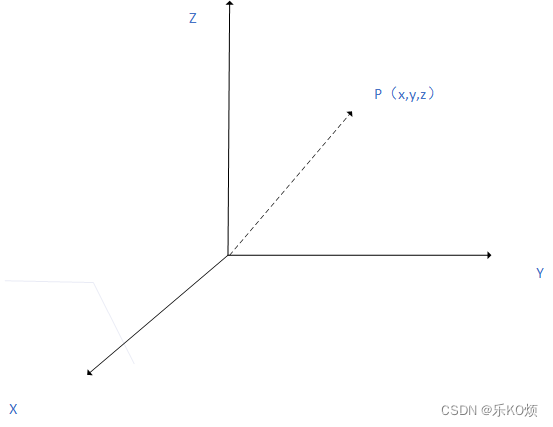
可以通过右手定则确定是右手坐标系。
确定轴的旋转的正方向，用右手的大拇指指向轴的正方向，弯曲手指手指。手指方向即是轴的正旋转方向。
2.坐标轴绕z轴旋转
坐标轴绕z轴正向旋转相当于op向量在xoy平面上顺时针旋转：
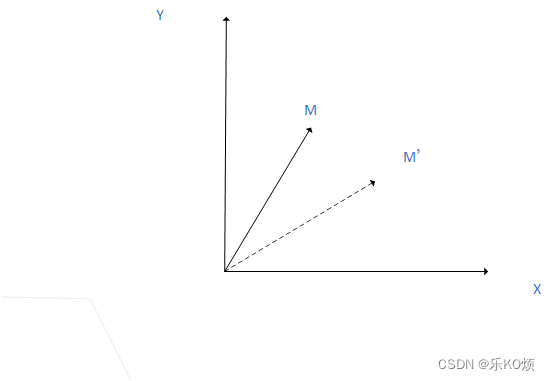
则可以推导出
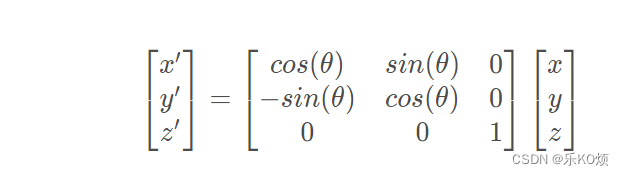
其中M’坐标(x’,y’,z’）；M坐标(x,y,z)
3.绕X轴旋转
同理绕X轴正向旋转相当于如下图的向量旋转。
[
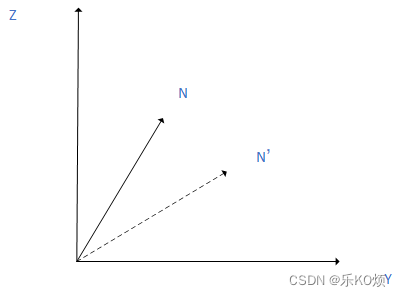
x
′
y
′
z
′
]
=
[
1
0
0
0
c
o
s
(
θ
)
s
i
n
(
θ
)
0
−
s
i
n
(
θ
)
c
o
s
(
θ
)
]
[
x
y
z
]
\begin{bmatrix} x' \\ y' \\z' \end{bmatrix} = \begin{bmatrix} 1&0& 0 \\ 0&cos(\theta) & sin(\theta) \\ 0&-sin(\theta) & cos(\theta) \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}
⎣⎡x′y′z′⎦⎤=⎣⎡1000cos(θ)−sin(θ)0sin(θ)cos(θ)⎦⎤⎣⎡xyz⎦⎤
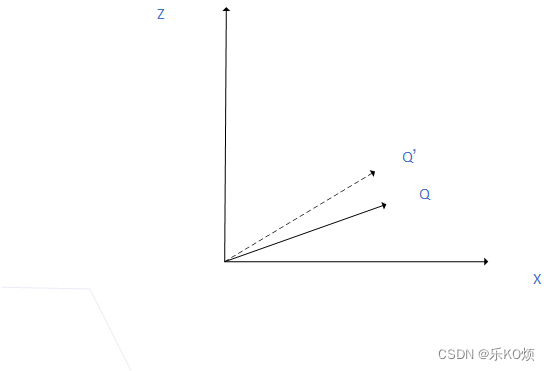
4. 绕Y轴旋转
绕Y轴正向旋转相当于下图
[
x
′
y
′
z
′
]
=
[
c
o
s
(
θ
)
0
−
s
i
n
(
θ
)
0
1
0
s
i
n
(
θ
)
0
c
o
s
(
θ
)
]
[
x
y
z
]
\begin{bmatrix} x' \\ y' \\z' \end{bmatrix} = \begin{bmatrix} cos(\theta) & 0&-sin(\theta) \\ 0&1& 0 \\ sin(\theta) & 0& cos(\theta) \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}
⎣⎡x′y′z′⎦⎤=⎣⎡cos(θ)0sin(θ)010−sin(θ)0cos(θ)⎦⎤⎣⎡xyz⎦⎤
5.绕X,Y,Z轴正向旋转
绕X,Y,Z轴，坐标系正向旋转，所需要的旋转矩阵是
2747
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
